PERÍMETRO, ÁREA Y VOLUMEN UTILIZANDO FÓRMULAS
MATEMATICAS
Aprendizajes esperados:
- Calcular el perímetro de polígonos y del círculo, y áreas de triángulos y cuadriláteros desarrollando y aplicando fórmulas.
- Calcular el volumen de prismas rectos cuya base sea un triángulo o un cuadrilátero, desarrollando y aplicando fórmulas.
Cosas que necesito saber
En este apartado daré a conocer algunas cosas que se necesitan saber del tema y que son necesarios conocer para poder realizarlas.
1.-Conocer los conceptos de perímetro, volumen y área.
Perímetro: El perímetro es la suma de todos los lados. El término puede ser utilizado tanto para la distancia o longitud, como para la longitud del contorno de una forma. El perímetro de un círculo se llama longitud de la circunferencia.
2.- Reconocer los diferentes polígonos que hay.
Los polígonos son lo que se entiende en geometría como figuras planas con
un determinado número de lados que engloban una región de un plano de
manera finita. Esos costados que forman los segmentos de la figura se conocen
como aristas y el punto en el que se juntan dos aristas se llama vértice o
esquina. En cada uno de esos vértices se generan dos ángulos, el interior y el
exterior, que simplemente es la amplitud generada en el vértice.
Hay distintas clasificaciones para los polígonos, pero en este artículo
hablaremos de los polígonos regulares y los irregulares.
- Polígonos regulares: Son aquellos que tienen todos los ángulos de la misma amplitud y todos
los lados de la misma longitud.
- Polígonos irregulares: Son los que o bien tienen los costados de igual longitud, pero ángulos
de distinta amplitud; o bien tienen los costados de distinta longitud, pero
ángulos de idéntica amplitud; o bien tienen los costados de distinta longitud y
ángulos de distinta amplitud.
3.- Conocer cuáles son los polígonos regulares y numero de
lados.
- Triángulo
equilátero: 3
- Cuadrado: 4
- Pentágono irregular: 5
- Hexágono regular: 6
- Heptágono regular: 7
- Octógono u octágono regular: 8
- Eneágono o nonágono regular: 9
- Decágono regular: 10
- Endecágono o undecágono irregular: 11
- Dodecágono regular: 12
- Tridecágono o triskaidecágono regular: 13
- Tetradecágono regular: 14
- Pentadecágono o pentadecágono regular: 15
- Hexadecágono regular: 16
- Heptadecágono regular: 17
- Octodecágono u octadecágono regular: 18
- Eneadecágono o nonadecágono regular: 19
- Isodecágono o icoságono regular: 20
4.-Conocer los polígonos irregulares y numero de lados.
- Triángulo no equilátero: 3
- Cuadrilátero (rombo, rectángulo, romboide, trapecio, trapezoide): 4
- Pentágono irregular: 5
- Hexágono irregular: 6
- Heptágono irregular: 7
- Octógono u octágono irregular: 8
- Eneágono o nonágono irregular: 9
- Decágono irregular: 10
- Endecágono o undecágono irregular: 11
- Dodecágono irregular: 12
- Tridecágono o triskaidecágono irregular: 13
- Tetradecágono irregular: 14
- Pentadecágono o pentadecágono irregular: 15
- Hexadecágono irregular: 16
- Heptadecágono irregular: 17
- Octodecágono u octadecágono irregular: 18
- Eneadecágono o nonadecágono irregular: 19
- Isodecágono o icoságono irregular: 20
5.-Conocer las fórmulas para poder encontrar perímetro de polígonos.
6.-Conocer la fórmula para perímetro de un circulo.
L = 2 · π · r
Es decir, deberemos multiplicar por dos el número pi y la longitud del radio de la circunferencia o, lo que sería lo mismo, multiplicar pi por el diámetro de la circunferencia, porque el diámetro mide el doble que el radio (y omitimos así multiplicarlo por dos).
7.- Diferencia entre circunferencia y círculo.
- Circunferencia se refiere a la curva cerrada cuyos puntos son todos equidistantes del centro situado en un plano.
- Círculo es el área contenida dentro de los puntos de la circunferencia.
8.- Conocer la fórmula para calcular área de triángulos.
9.- conocer las figuras geométricas.
10.- Saber sacar el área de cuadriláteros.
Rombo. Existen varias fórmulas para calcular el área de un rombo. La más común es mediante las dos diagonales del rombo (las diagonales de un rombo son perpendiculares). El área es la mitad del producto de las diagonales (D y d).
Romboide. El área de un romboide es el resultado de multiplicar la base por la altura (h). Dicha altura es un segmento perpendicular a b que mide la distancia de b a su lado paralelo.
Trapecio. El área del trapecio se calcula a partir de su altura y las dos bases. Es el resultado de la suma de las bases por la altura, y dividido entre dos.
11.- Saber que es un prisma recto con base triangular.
prisma triangular regular:
Un prisma triangular tiene 5 caras (2 bases y 3 caras laterales), 9 aristas y 6 vértices.
La altura del prisma es la distancia entre las dos bases (coincide con la longitud de las aristas laterales en el caso del prisma recto).
Como las bases son iguales, las caras laterales son rectangulares.
12.- Saber la fórmula para sacar volumen de prismas rectos con base de triangular.
Ab= área de la base
H= altura
13.- Saber la formula para sacar el volumen de prisma recto con base de Cuadriláteros.
A continuación se presenta la formula para calcular el volumen del prisma con base cuadrada, y un ejemplo para que puedas entenderlo mejor y ponerlo en práctica.
Cosas que no necesito saber
Hay cosas que no necesariamente necesitamos saber o conocer para llegar al aprendizaje esperado de este tema en particular, a continuación te mostrare algunas de estas:
1.- De donde proviene pi (historia).
2.-Nombre griego de perímetro.
3.- El semiperímetro.
4.-Historia del área y porque la crearon.
5.- Método exhaustivo.














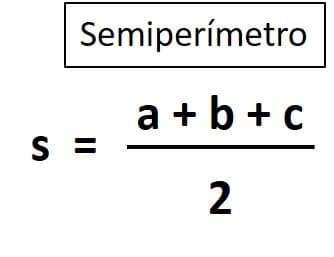

¡Hola Alejandra! Haces buena clasificación de los conceptos tales como los tipos de polígonos y das una definición formal de cada concepto, eso es bueno, porque, por ejemplo, muchas veces confundimos el concepto de circunferencia y circulo, que por definición son cosas muy distintas. Tienes razón al decir que no necesitamos saber el origen del pi ni la demostración de fórmulas, pero dentro de lo que cabe en este tema es saber operar bien con los números, en mi opinión, trabajar con fórmulas sustituyendo valores en las variables para luego evaluarlas, es el primer paso que damos para acercarnos al algebra, de hecho ya es una operación algebraica porque empezamos a manejar el pi como una constante en las formulas, por esta razón creo que antes que nada se debe saber sumar, restar, dividir y multiplicar, de hecho las mismas formulas indican las operaciones que debemos hacer para llegar al resultado.
ResponderEliminarHola Alejandra, me gustó tu trabajo es un trabajo concreto, me gusta que específicaste de que trata cada punto eso ayuda a darse una idea del que si lo necesitas o no saber, me llama la atención el uso de material audiovisual que utilizaste auque faltó un poco de eso en el apartado que no debo saber pero es bastante preciso y entendible ya que das una explicación de qué trata en cada punto por lo que aún así es entendible, buen trabajo compañera.
ResponderEliminar¡Hola Ale!, Considero que hiciste un buen trabajo, pues la información que presentas es bastante concreta y clara.
ResponderEliminarA mí parecer está todo bien organizado, además de que pusiste una definición de cada concepto que incluye tu tema, eso ayuda a esclarecer ciertas dudas en cuanto a los términos. Las imágenes son bastante llamativas, ya que incluyen las fórmulas que se necesitan para obtener resultados.
Y por supuesto los ejemplos que pusiste son de gran importancia pues facilitan la comprensión de las fórmulas para sacar el área y el Volumen de distintas figuras y cuerpos geométricos.
Toda la información planteada es muy buena, a veces solo es de forma mecanizada al momento de resolver áreas, perímetros y volúmenes, pero en realidad omitimos muchos conceptos bases que deben ser tomados en cuenta y es muy bueno que seas especifica en todo lo que se debe saber y también en lo que no se debe saber, ya que es muy comprensible cada punto y no lo dejas a la deriva. ¡felicidades!
ResponderEliminarQue Llamativo y hermoso trabjo. Muy buen y claro contenido el que abordas, de verás me gustó mucho tu blog. El tema que abordas es uno que muchas veces suele ser mecanizado por los doscentes pero a¿dentro de tu contenido veo que usaste otras estretegias. Muy buen contenido Ale.
ResponderEliminar